Một bài toán tính tổng

Link bài toán: http://vn.spoj.com/problems/C11CAL/

Solution 0.00s
Đọc bài này, cái mình nghĩ đến đầu tiên là auto sinh lời giải (vì k nhỏ quá), chạy Maple giải cho toàn bộ k dưới 50, ta có solution 0.00s:

Solution nhân ma trận
Sau đó do cắn rứt lương tâm quá 🙁 Sao mình giải 0.00s mà ng khác giải lại cả 40-50s, mình thử giải cách chính thống chút). Đặt S_n^k = \sum_{i=1}^n{i^k}. Để có thể áp dụng nhân ma trận, ta cần biến đổi bài toán về dạng tuyến tính X_{n+1} = A X_n với X_i là một vector (trạng thái), A là ma trận (chuyển đổi trạng thái).
Ta có S_{n+1}^k - S_n^k = (n+1)^k, hàm này không thể tìm được ma trận A nào thoả mãn, mình phải thêm các giá trị trung gian để giúp việc biến đổi trở thành tuyến tính.
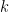Mặt khác, (n+1)^k = n^k + C_k^1 n^{k-1} + C_k^2 n^{k-2} + ... + C_k^1 n + 1, ta có thể tính được (n+1)^k một cách tuyến tính từ k luỹ thừa tự nhiên đầu tiên của n, đặt X_i = \left[ 1, i, i^2, ..., i^k, S_i^k \right]^T, ta được:

\begin{vmatrix} 1\\i+1\\(i+1)^2\\\vdots\\(i+1)^k \end{vmatrix} = \begin{vmatrix} C_0^0 & 0 & 0 & \hdots & 0\\ C_1^0 & C_1^1 & 0 & \hdots & 0\\ C_2^0 & C_2^1 & C_2^2 & \hdots & 0\\ \vdots & \vdots & \vdots & \ddots & \\ C_k^0 & C_k^1 & C_k^2 & \hdots & C_k^k \end{vmatrix} \begin{vmatrix} 1\\i\\i^2\\\vdots\\i^k \end{vmatrix}

Lúc này S_{n+1}^k = S_{n}^k + (n+1)^k = S_{n}^k + n^k + C_k^1 n^{k-1} + C_k^2 n^{k-2} + ... + C_k^1 n + 1, ta chỉ cần thêm 1 giá trị vào vector trạng thái:

\begin{vmatrix} 1\\i+1\\(i+1)^2\\\vdots\\(i+1)^k\\S_{i+1}^k \end{vmatrix} = \begin{vmatrix} C_0^0 & 0 & 0 & \hdots & 0 0\\ C_1^0 & C_1^1 & 0 & \hdots & 0 0\\ C_2^0 & C_2^1 & C_2^2 & \hdots & 0 0\\ \vdots & \vdots & \vdots & \ddots & \\ C_k^0 & C_k^1 & C_k^2 & \hdots & C_k^k 0 C_k^0 & C_k^1 & C_k^2 & \hdots & C_k^k 1 \end{vmatrix} \begin{vmatrix} 1\\i\\i^2\\\vdots\\i^k\\S_{i}^k \end{vmatrix}

Solution khử Gauss
Bài này còn có thể nhận xét S_n^k là một đa thức bậc k+1, ta có thể tính ra đa thức đó bằng cách giải hệ phương trình bằng thuật toán khử Gauss trên \mathbb{Z}/(1000000007).